Sample Problems > Applications > Fluids > 1d_eulerian

{ 1D_EULERIAN_SHOCK.PDE

Comparison with shock tube problem of G.A. Sod

See 1D_LAGRANGIAN_SHOCK.PDE for a Lagrangian model of the same problem.

Ref: G.A. Sod, "A Survey of Several Finite Difference Methods for Systems of

Nonlinear Hyperbolic Conservation Laws", J. Comp. Phys. 27, 1-31 (1978)

See also Kershaw, Prasad and Shaw, "3D Unstructured ALE Hydrodynamics with the

Upwind Discontinuous Finite Element Method", UCRL-JC-122104, Sept 1995.

}

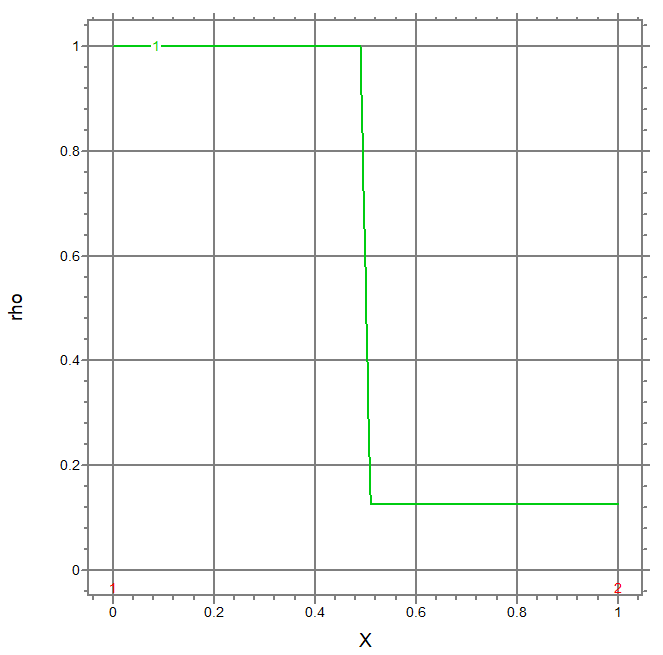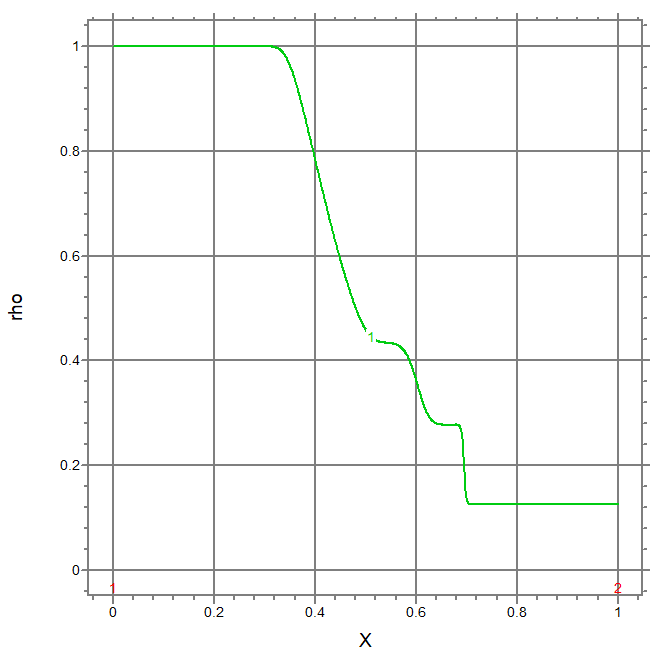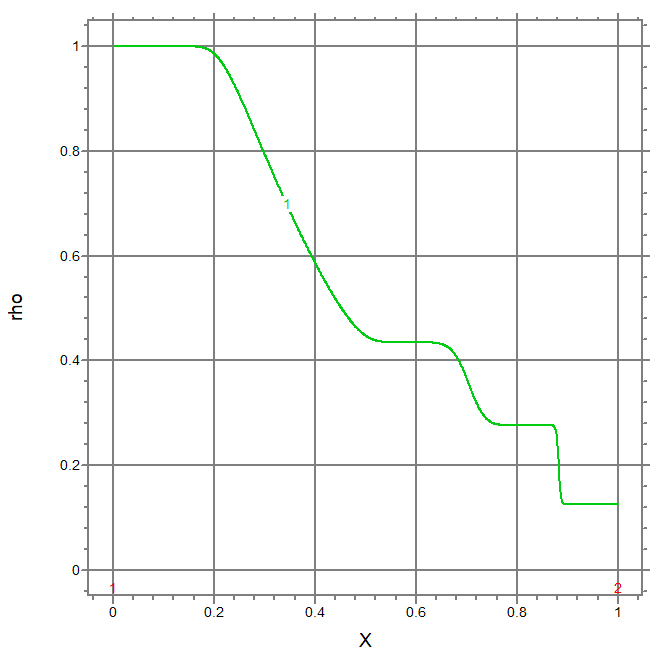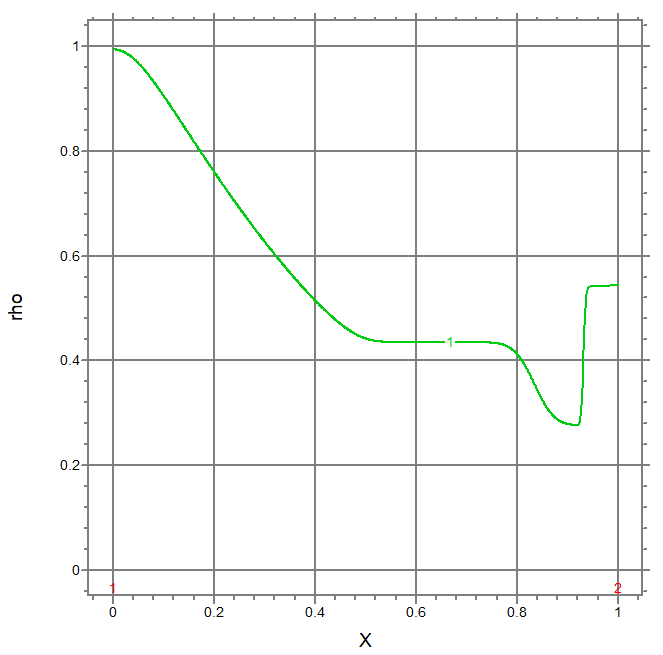
TITLE "Sod's Shock Tube Problem - Eulerian"

COORDINATES

cartesian1

SELECT

ngrid=200 { increase the grid density }

regrid=off { disable the adaptive mesh refinement }

errlim=1e-4 { lower the error limit }

VARIABLES

rho(1)

u(1)

P(1)

DEFINITIONS

len = 1

gamma = 1.4

smeardist = 0.001 { a damping term to kill unwanted oscillations }

eps = sqrt(gamma)*smeardist { ~ cspeed*dist }

INITIAL VALUES

rho = 1.0 - 0.875*uramp(x-0.49, x-0.51)

u = 0

P = 1.0 - 0.9*uramp(x-0.49, x-0.51)

EQUATIONS

rho: dt(rho) + u*dx(rho) + rho*dx(u) = eps*dxx(rho)

u: dt(u) + u*dx(u) + dx(P)/rho = eps*dxx(u)

P: dt(P) + u*dx(P) + gamma*P*dx(u) = eps*dxx(P)

BOUNDARIES

REGION 1

START(0) point value(u)=0

Line to (len) point value(u)=0

TIME 0 TO 0.375

MONITORS

for cycle=5

elevation(rho) from(0) to (len)

elevation(u) from(0) to (len)

elevation(P) from(0) to (len)

history(rho) at (0.5)

history(u) at (0.48) (0.49) (0.5) (0.51) (0.52)

history(p) at (0.48) (0.49) (0.5) (0.51) (0.52)

history(deltat)

grid(x)

PLOTS

for t=0.143, 0.375