Technical Notes > Applications in Electromagnetics > Magnetostatics

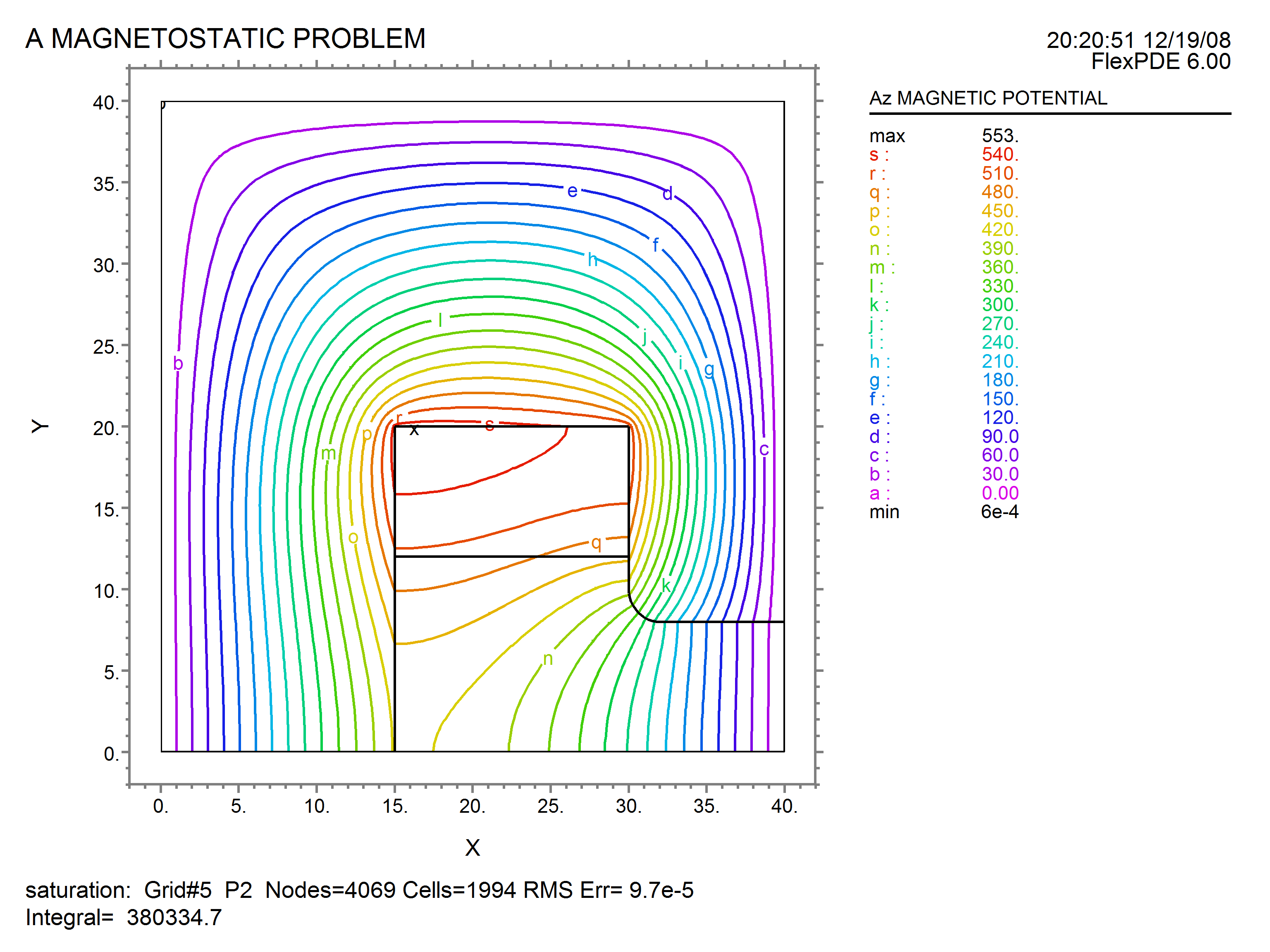
In the following 2D Cartesian example, a current-carrying copper coil is surrounded by a ferromagnetic core with an air gap. Current flows in the coil in the Z direction (out of the computation plane), and only the Z component of the magnetic vector potential is nonzero. The Coulomb gauge condition is again satisfied automatically. We assume a symmetry plane along the X-axis, and impose along the remaining sides. The relative permeability is in the air and the coil, while in the core it is given by
,
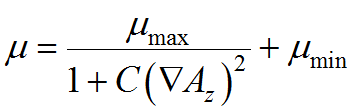with parameters giving a behavior similar to transformer steel.

Descriptor 2.2: Saturation.pde

Title "A MAGNETOSTATIC PROBLEM"

Select

errlim = 1e-4

Variables

Definitions

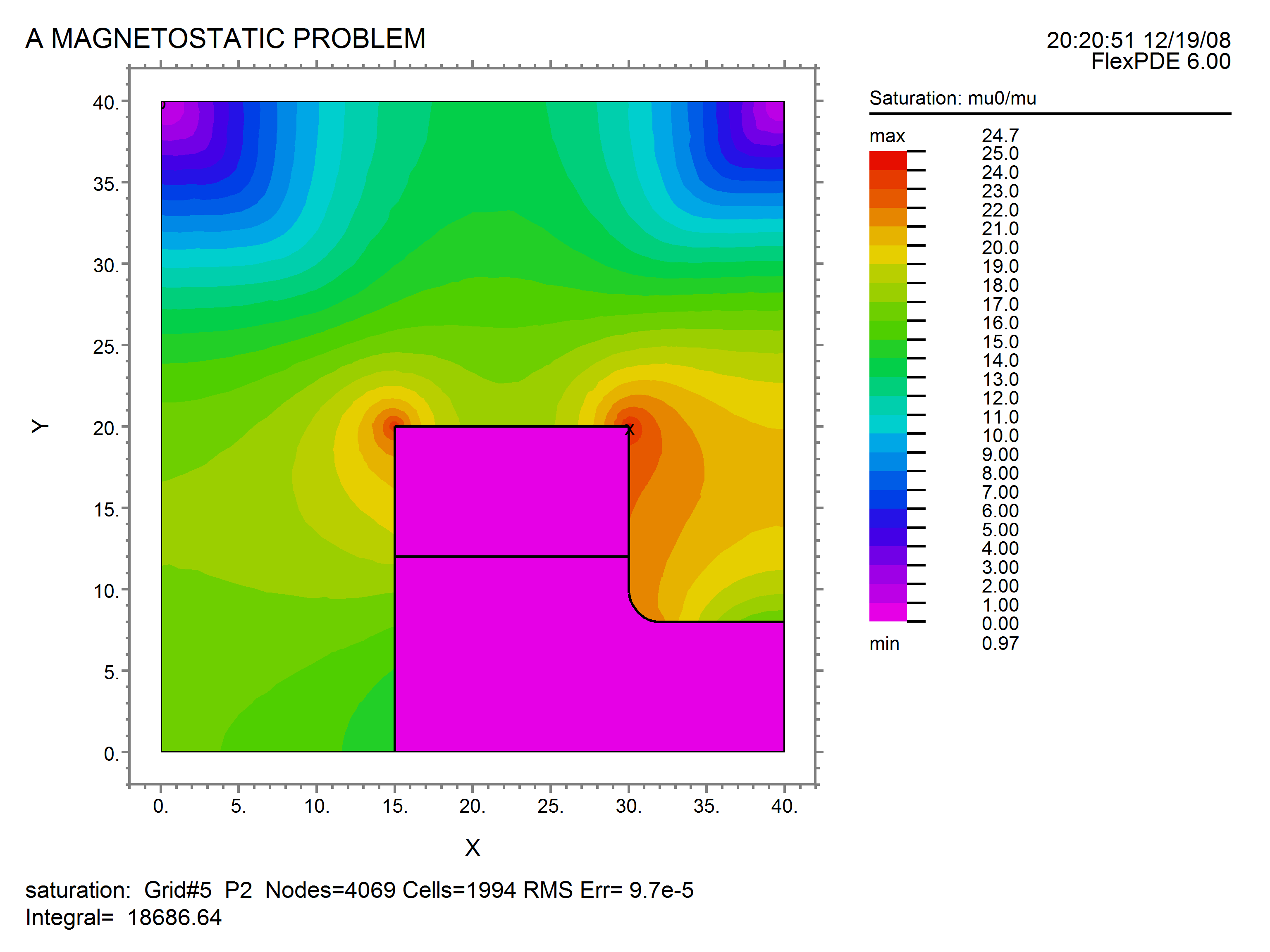
mu = 1 { default to air}

mu0 = 1 { for saturation plot }

mu_max = 5000

mu_min = 200

mucore = mu_max/(1+0.05*grad(A)^2) + mu_min

S = 0

current = 2

y0 = 8

Equations

curl(curl(A)/mu) = S

Boundaries

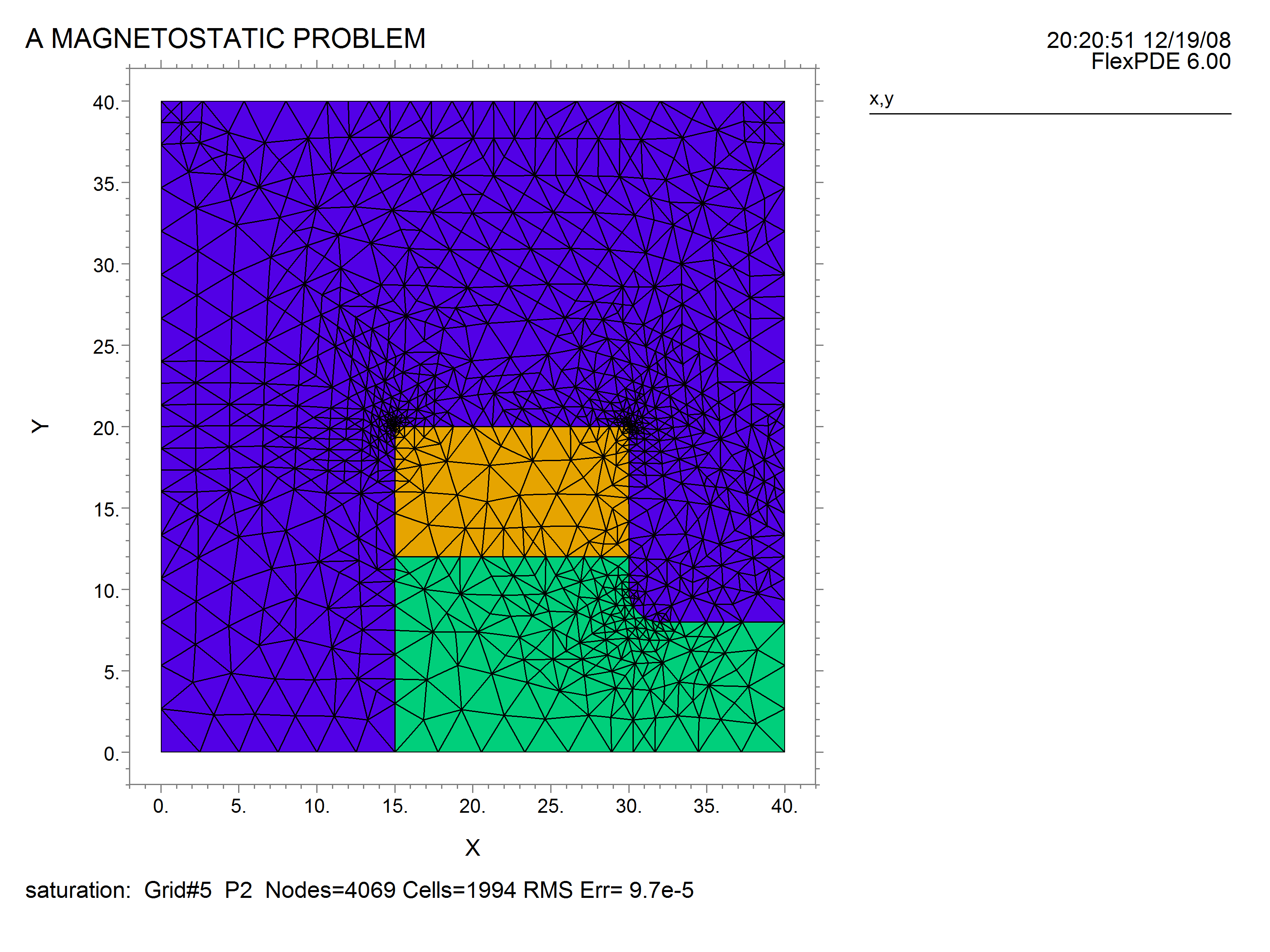
Region 1 { The IRON core }

mu = mucore

mu0 = mu_max

start(0,0)

natural(A) = 0 line to (40,0)

value(A) = 0 line to (40,40) to (0,40) to close

Region 2 { The AIR gap }

mu = 1

start (15,0)

line to (40,0) to (40,y0) to (32,y0)

arc (center=32,y0+2) to (30,y0+2)

line to (30,20) to (15,20) to close

Region 3 { The COIL }

S = current

mu = 1

start (15,12)

line to (30,12) to (30,20) to (15,20) to close

Monitors

contour(A)

Plots

grid(x,y)

vector(dy(A),-dx(A)) as "FLUX DENSITY B"

vector(dy(A)/mu, -dx(A)/mu) as "MAGNETIC FIELD H"

contour(A) as "Az MAGNETIC POTENTIAL"

surface(A) as "Az MAGNETIC POTENTIAL"

contour(mu0/mu) painted as "Saturation: mu0/mu"

End

Nonlinear Permeability in 2D

Nonlinear Permeability in 2D

Descriptor 2.2: Saturation.pde